|

|
|
Les G : |
Les G sont en faite liés au poids d’un solide en mouvement et subissant une accélération. Ils se présentent sous différentes manières que nous allons montrer par la suite.
Il faut donc tout d’abord commencer par dire que :
Dans un référentiel non galiléen d’accélération, un corps uniquement soumis au champ de gravitation 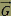 subit un champ de pesanteur défini par : subit un champ de pesanteur défini par : 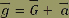
Dans le cas présent,  représente l’accélération de l’avion. Sachant que représente l’accélération de l’avion. Sachant que 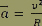
|
 |
Le pilote subit donc d’une part le champ de gravitation terrestre 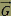 et d’autre part, le champ de pesanteur et d’autre part, le champ de pesanteur  dû à l’accélération de l’avion. dû à l’accélération de l’avion.
Si l’accélération  est modifiée, c’est alors le vecteur champ de pesanteur est modifiée, c’est alors le vecteur champ de pesanteur  qui sera modifiée. qui sera modifiée.
Le champ de pesanteur subi est caractérisé entre autre par son intensité. Plutôt que d’exprimer cette intensité en m.s-2 ou en N.kg-1, on l’exprime habituellement en prenant comme référence l’intensité du champ de pesanteur terrestre, égale à 9,81 m.s-2.
C'est-à-dire que pour 2G, le champ de pesanteur (du pilote ou de l’avion) sera égal à 2 fois celui de la terre.
Nous allons donc étudier les accélérations en avion, et pour ceci on distinguera 2 cas : les G positifs et les G négatifs.
On peut en effet décomposer le vecteur 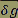 en trois composantes : longitudinale, transversale et latérale. en trois composantes : longitudinale, transversale et latérale.
|
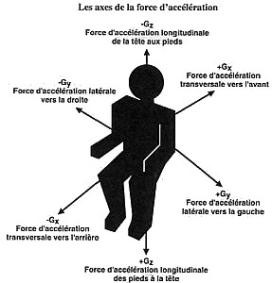 |
Les G Positifs :
|
 |
Soit 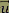 un vecteur unitaire dirigé du haut vers le bas de l’avion. un vecteur unitaire dirigé du haut vers le bas de l’avion.
On parle de G positifs lorsque le produit scalaire 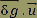 est positif. est positif.
Le produit scalaire 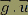 , qui représente la composante longitudinale du champ de pesanteur, est exprimé en Gz (ou G longitudinaux). , qui représente la composante longitudinale du champ de pesanteur, est exprimé en Gz (ou G longitudinaux).
Exemple : L’avion effectue un Looping (Boucle vertical)
L’accélération  subie par l’avion est dirigée vers le haut. subie par l’avion est dirigée vers le haut.
Le champ de pesanteur  qui en résulte est donc dirigé vers le bas de l’avion.
Le produit scalaire qui en résulte est donc dirigé vers le bas de l’avion.
Le produit scalaire 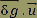 est positif, il s'agit donc de G positifs. est positif, il s'agit donc de G positifs. |
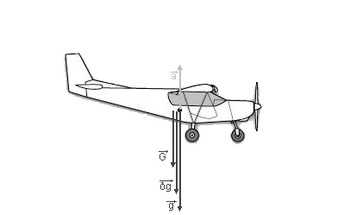 |
Sur ce schéma, les vecteurs allant vers le bas ne sont confondus, en réalité ils doivent l’être mais c’est pour une meilleure lecture de ceux-ci.
Exprimons le champ de pesanteur subi lorsque l’avion est à la fin de la manœuvre (en supposant sa vitesse constante) :
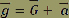
En projetant sur l’axe des ordonnées :
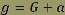

Par exemple, si l’avion effectue sa boucle a une vitesse de 70 m.s-2 (250 Km.h-1) et un rayon de courbure de 500m, le champ de pesanteur subi sera de :
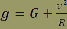

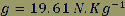 ou ou 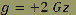
Le pilote subit donc un champ de pesanteur d’une intensité 2 fois supérieure à celle du champ de pesanteur terrestre. Il « pèse 2 fois » son poids habituel.
|
Les G Négatifs :
|
 |
On parle de G négatifs lorsque le produit scalaire 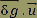 exprimé en Gz est négatif. exprimé en Gz est négatif.
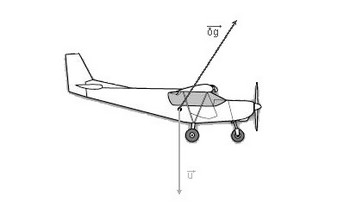
Exemple : L’avion pique du nez
L’accélération  subie par l’avion est dirigée vers le bas. subie par l’avion est dirigée vers le bas.
Le champ de pesanteur 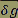 qui en résulte est donc dirigé vers le haut de l’avion. qui en résulte est donc dirigé vers le haut de l’avion.
Le produit scalaire 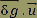 est négatif, il s'agit donc de G négatifs. est négatif, il s'agit donc de G négatifs.
|
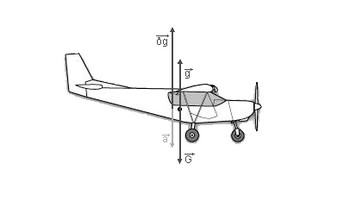 |
Sur ce schéma, les vecteurs allant vers le bas ainsi que ceux allant vers le haut ne sont confondus, en réalité ils doivent l’être mais c’est pour une meilleure lecture de ceux-ci.
Exprimons le champ de pesanteur subi lorsque l’avion est au sommet de sa trajectoire (en supposant sa vitesse constante) :
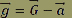
En projetant sur l'axe des ordonnées :
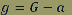

Par exemple, à la vitesse de 300 m.s-1 (soit 540 km/h) et avec un rayon de courbure de 4500 m:
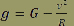

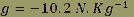 ou ou 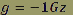
Dans ce cas ci, le pilote subit un champ de pesanteur dirigé vers le haut de son corps, d’intensité égale à celle du champ de pesanteur terrestre, mais il aura l’impression d’être « à l'envers ».
|
|
|

